| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- TIL #Today I Learned #
- hackerrank #python #algorithm #해커랭크 #파이썬 #알고리즘
- 블로그만들기 #웹사이트만들기 #
- javascript '===' #javascript #TIL #Today I Learned #기록 #회고
- 웹페이지제작 #
- javascript #event #onclick #js
- #TIL #Today I Learned #기록 #회고 #ternary statement #swich statement #스위치 반복문 #
- 강의 #느낀점 #snowfox #스노우폭스 #김승호회장
- 불리언 #Boolean #number #string #symbol #null #undefined
- TIL #Today I Learned # 기록 # 회고 #Udemy
- 블로그 셀프제작
- single source of truth란 #single source of truth #자료의중복 #자료의비정합성 #비정합성 #리팩토링
- 자바스크립트 #javascript #datatype #데이터타입 #자료형
- Hackerrank #해커랭크 #python #파이썬 #알고리즘 #Algorithm
- 고스트 블로그 #
- javascript #statement #expression #difference
- 기록 #회고
- Today
- Total
well-balanced
알고리즘 - 시간복잡도 (Time complexity) 본문
알고리즘 평가법
알고리즘을 공부할 때는 시간(time)과 공간(space)를 신경써야 한다.
비교적 더 중요하게 여겨지는 것은 시간인데 이를 측정하기 위해서 컴퓨터 과학에서는 시간복잡도(Time complexity)라는 개념을 사용한다.
Input의 크기에 따라 걸리는 시간이 빠를수록 시간복잡도가 작다고 표현하며, 더 빠른 알고리즘을 뜻한다.
알고리즘을 평가할 때는 점근 표기법(Big O 표기법)을 사용한다.
점근 표기법의 핵심은 크게 두가지인데 간단한 개념이다.
- n이 무수히 크다고 가정한다.
- 앞에 붙는 상수를 고려하지 않는다.
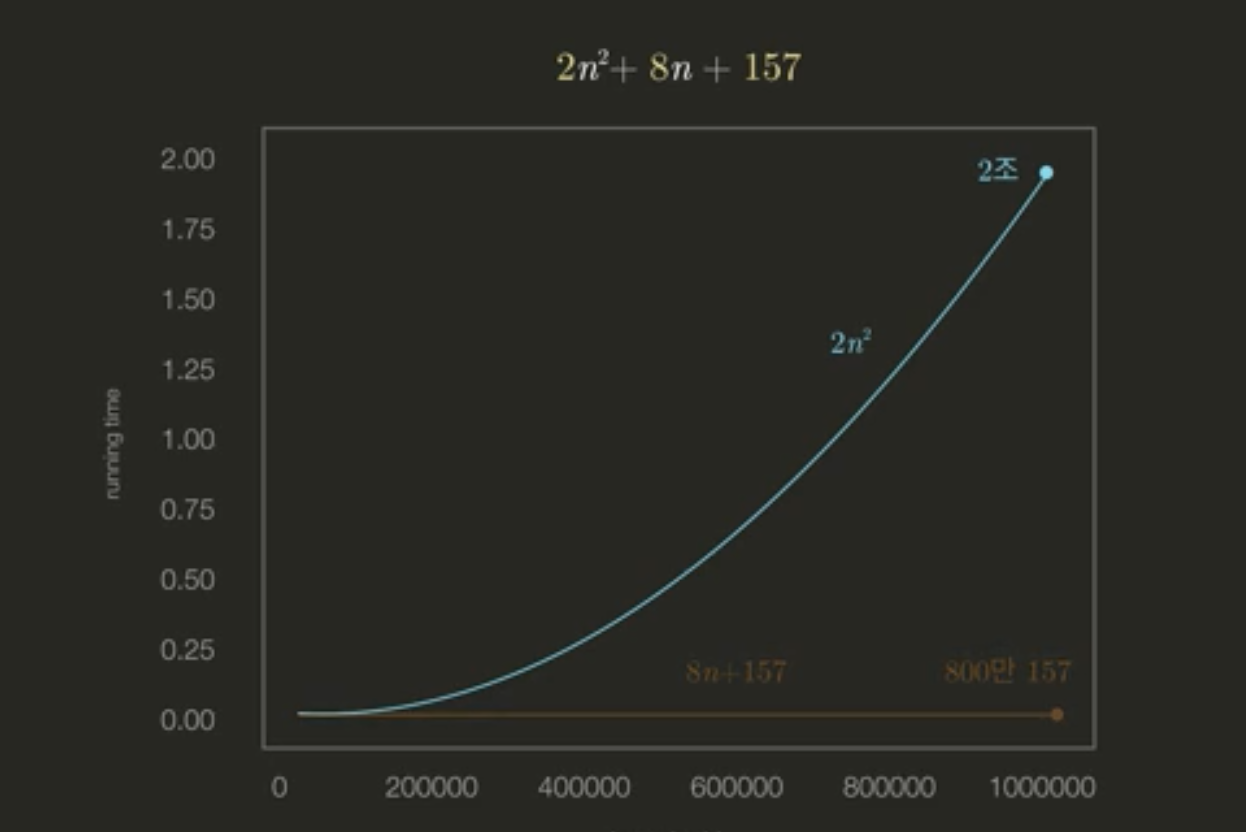
차수가 낮은 n이나 상수들은 Input이 무수히 커졌을 때 차수가 높은 n과 비교했을 때 Running time이 거의 신경쓰지 않아도 될 정도이기 때문에 Big O 표기법에서는 항상 n의 차수만을 고려한다.
아래의 그림들을 보면 Input의 길이와 Big O 표기법의 관계를 쉽게 이해할 수 있다.
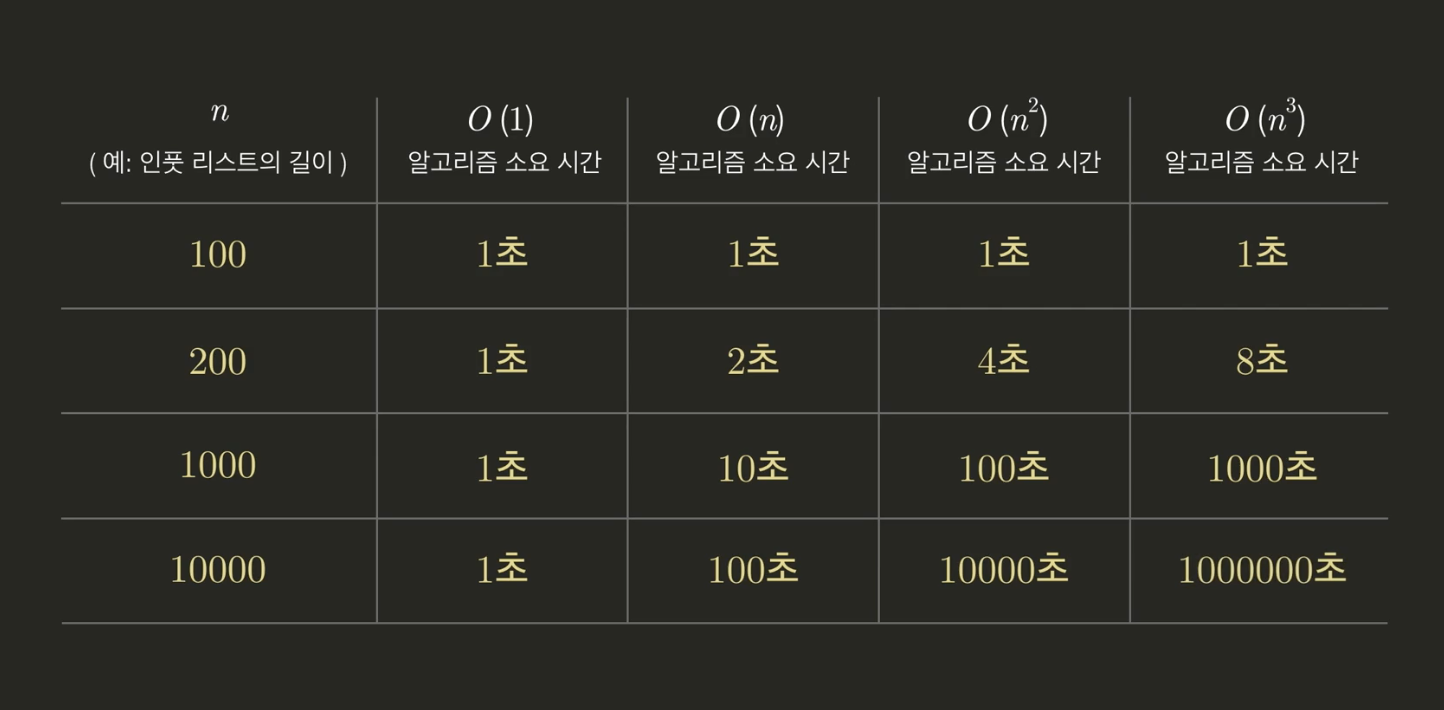

탐색 알고리즘을 예로 평가한다면 Big O 표기법으로 어떻게 나타낼 수 있을까?
Linear Search(선형 탐색)
def linear_search(element, arr):
for i in range(len(arr)): # O(n)
if element == arr[i]:
return i
return NoneBinary Search(이진 탐색)
def binary_search(element, arr):
start = 0
end = len(arr)
while True: # O(lg n), binary_search는 리스트의 길이만큼 순회하지 않고, 비교 연산을 통해 절반씩 잘라가면서 순회하기 때문
middle = (start + end) // 2
if element == arr[middle]:
return middle
elif element < arr[middle]:
end = middle
elif element > arr[middle]:
start = middle
if middle == 0 or middle == len(arr) - 1:
break
return None리스트의 각종 함수에 대한 평균 시간복잡도
# 인덱싱: O(1)
# 정렬: O(nlgn) (정렬마다 다름)
# 뒤집기: O(n)
# 선형탐색: O(n)
# 끝에 요소 추가: O(1)
# 중간에 요소 추가: O(n)
# 삭제: O(n)
# 최솟값, 최댓값 찾기: O(n)
# 길이: O(1)대체로 반복문이 없다면 O(1)이다.
반복문이 있고, 횟수가 Input의 크기와 비례한다면 일반적으로 O(n)이다.
for i in range(arr):
print(i)반복문이 연속으로 나오는 경우에는 O(n²), O(n³) 반복문의 횟수만큼 n의 지수로 붙는다.
for i in range(arr):
for j in range(arr):
for k in range(arr):
...Binary Search(위 코드 참고)와 같이 List의 크기가 반복할 때마다 절반씩 줄어드는 경우는 O(lg n)
아래 코드와 같이 반복문 안에 O(lg n) 반복문이 있을 때 O(nlgn)
def print_powers_of_two_repeatedly(n):
for i in range(n): # 반복횟수: n에 비례
j = 1
while j < n: # 반복횟수: lg n에 비례
print(i, j)
j = j * 2'Algorithm' 카테고리의 다른 글
| 알고리즘 - 재귀함수 (Recursive Function) (0) | 2020.04.10 |
|---|

